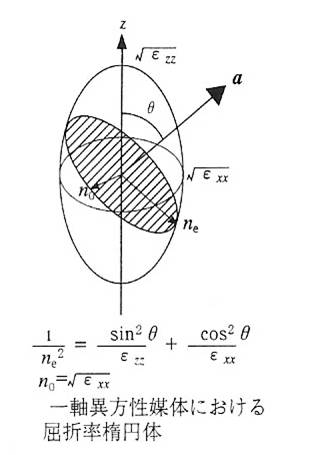
E=E0e-iωt+ikx =E0 exp{-iωt+ikx} (1)
で表されます。上式においてkは波数とよばれ、空間的な周波数をあらわします。波長をλとすると、波数は波長λの逆数に2πをかけたものとして定義されます。従ってk=2π/λ です。前に述べたようにk=ω/vですが、媒体中ではvが光速の屈折率n分の1になっています。すなわち、v=c/nですから、
k=nω/c (2)
と表されます。光速cは周波数 ω/2πと波長λの積なので、 k=2πn/λ=2π/(λ/n)と書くことができ、媒質中の光の波長が屈折率分の1になっていることと対応しています。吸収のある場合:複素数の屈折率の導入
現実の媒質では吸収が存在します。吸収を表す光学定数が消光係数κです。吸収がある場合は、波数を表す式(2)は屈折率nだけでは表すことができません。屈折率の代わりに、屈折率nを実数部、消光係数κを虚数部とする複素数の屈折率N=n+iκに置き換える必要があります。すなわち
k=Nω/c (3)
なぜこうするかというと、このように複素屈折率を導入すると波動を指数関数で表したときに都合がよいからです。(3)を(1)に代入すると、次式のようになります。 E=E0e-iωt+iNωx/c
=E0e-iωt+i(n+iκ)ωx/c
=E0e-iκωx/ce-iω(t-nx/c) (4)
消光係数κの意味
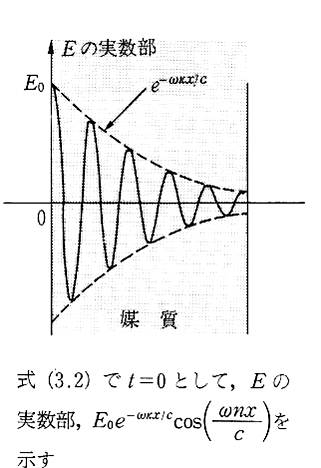 式(4)の、最初の因子e-κωx/cは振幅が距離とともに減衰していく様子を表し、二番目の因子e-iω(t-nx/c)が波の伝搬していく様子を表します。
式(4)の、最初の因子e-κωx/cは振幅が距離とともに減衰していく様子を表し、二番目の因子e-iω(t-nx/c)が波の伝搬していく様子を表します。光の強度Iは電界の振幅の絶対値の二乗に比例する量ですから、
I ∝ |E|2=E02e-2ωκx/c (5)
で表されます。この式は、光が物質中を 進むときに吸収を受けて弱くなっていく様子を表します。このように、κは光の減衰を表すので 消光係数(extinction coefficient)とよばれます。
消光係数と吸収係数
媒体による光の吸収の強さを表すのが吸収係数α[cm-1]です。吸収係数は入射光の強度が1/eになるまでに光が進む距離の逆数です。すなわち、媒体中を、0からx[cm]まで光が進んだとき、x=0においてI (0)であった光強度がxにおいてはI (x)になっていたとすると、
I (x)=I (0)e-αx (6)
として、吸収係数αが定義されます。吸収係数と消光係数の関係は、式(5)と式(6)を比較してα=2ωκ/c=4πκ/λ (7)
が得られます。ここにλは波長を表します。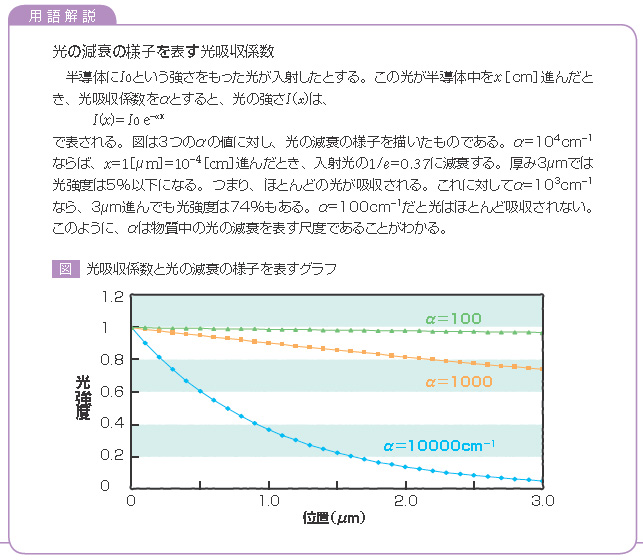
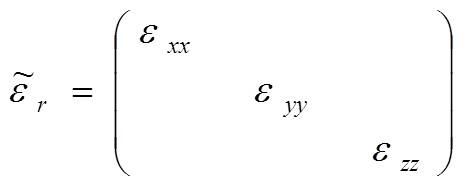 (16)
(16) (16')
(16')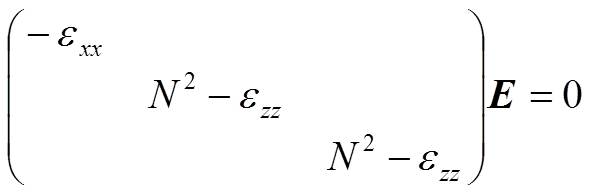 (17)
(17) (20)
(20)